逻辑回归(一):0还是1?
分类
对于人来说,分类是一种很自然的能力。看到猫的照片,我们知道是猫,看到狗的照片,我们知道是狗;根据邮件的内容我们也能很快看出这是不是一封广告/诈骗邮件。既然人能简单地完成这种任务,那我们能不能让计算机也做到呢?显然,当今的社会生活已经给了我们答案。我们今天就介绍一种最为简单的分类思想,逻辑回归(Logistic Regression)。
任务
首先,从简单的二分类讲起。
- 邮件:是否为诈骗邮件
- 肿瘤:良性还是恶性
- 照片:猫还是狗
类似这些的分类任务,我们称之为二分类(Binary Classification)。事实上这种二分类问题都可以抽象成对0和1的分类。整个模型简图如下,输入数据,通过一个函数,输出一个类别(0或者1)。

思路和方法
我们的思考方式一般都是从低维慢慢拓展至高维,所以我们这里就假设一个物体的特征可以用一个数来表示。比如我们假设根据肿瘤的大小就可以判断肿瘤是良性还是恶性,并且假设大的肿瘤更可能是恶性肿瘤。用0表示良性肿瘤,用1表示恶性肿瘤。
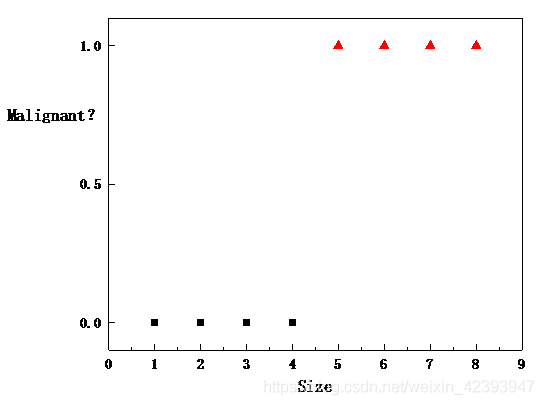
如上图所示,显然根据我们的设定,Size在1-4的 肿瘤都算是良性的肿瘤,Size大于等于5的肿瘤都是恶性的肿瘤。那么,根据这些数据,我们要怎么样才可以得到一个通用模型,使得输入一个肿瘤的大小,就可以判断它是良性的还是恶性的呢?
用线性回归?
按照这个思路,很容易联想到其实这也很像一个预测的过程,那么用我们之前介绍过的线性回归(线性回归:机器学习的"Hello, World")可不可以做到呢?
不妨试他一试,上图中的线性拟合结果大致可以表示成下图:
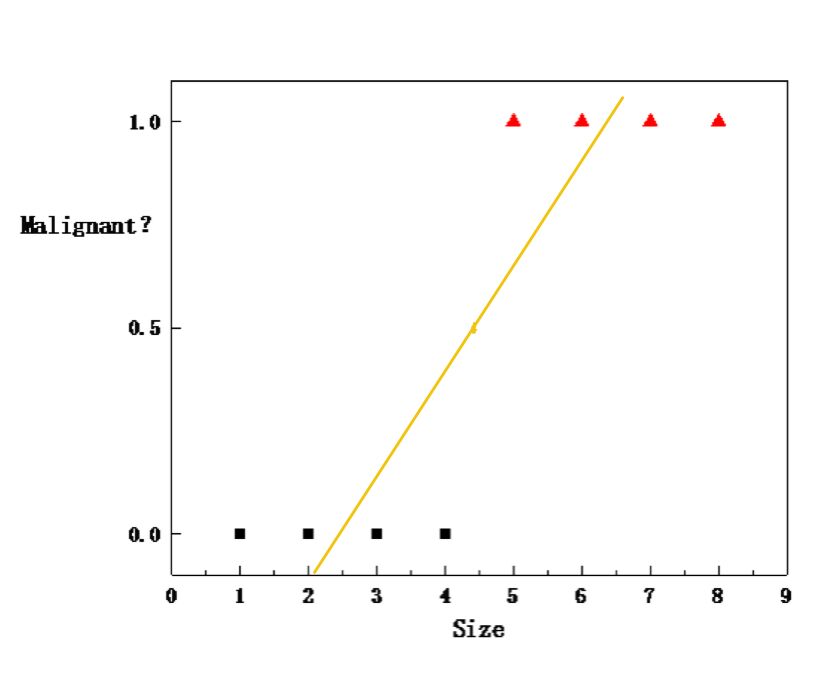
那么随便输入一个肿瘤的大小,我们就会得到一个输出\(h_{\theta}(x)\),但是这个值的范围并不只有0和1,这种情况要怎么办呢?我们可以取0和1的中点0.5作为一个阈值,根据以下规则调整输出:
- 如果\(h_{\theta}(x)\geq0.5\),认为\("y=1"\)
- 如果\(h_{\theta}(x)<0.5\),认为\("y=0"\)
这样看起来貌似挺合理的,但是如果我们再加一个比较偏远的数据点呢?这个时候我们的误差就会非常大了,所以显然这并不是一个特别好的选择。
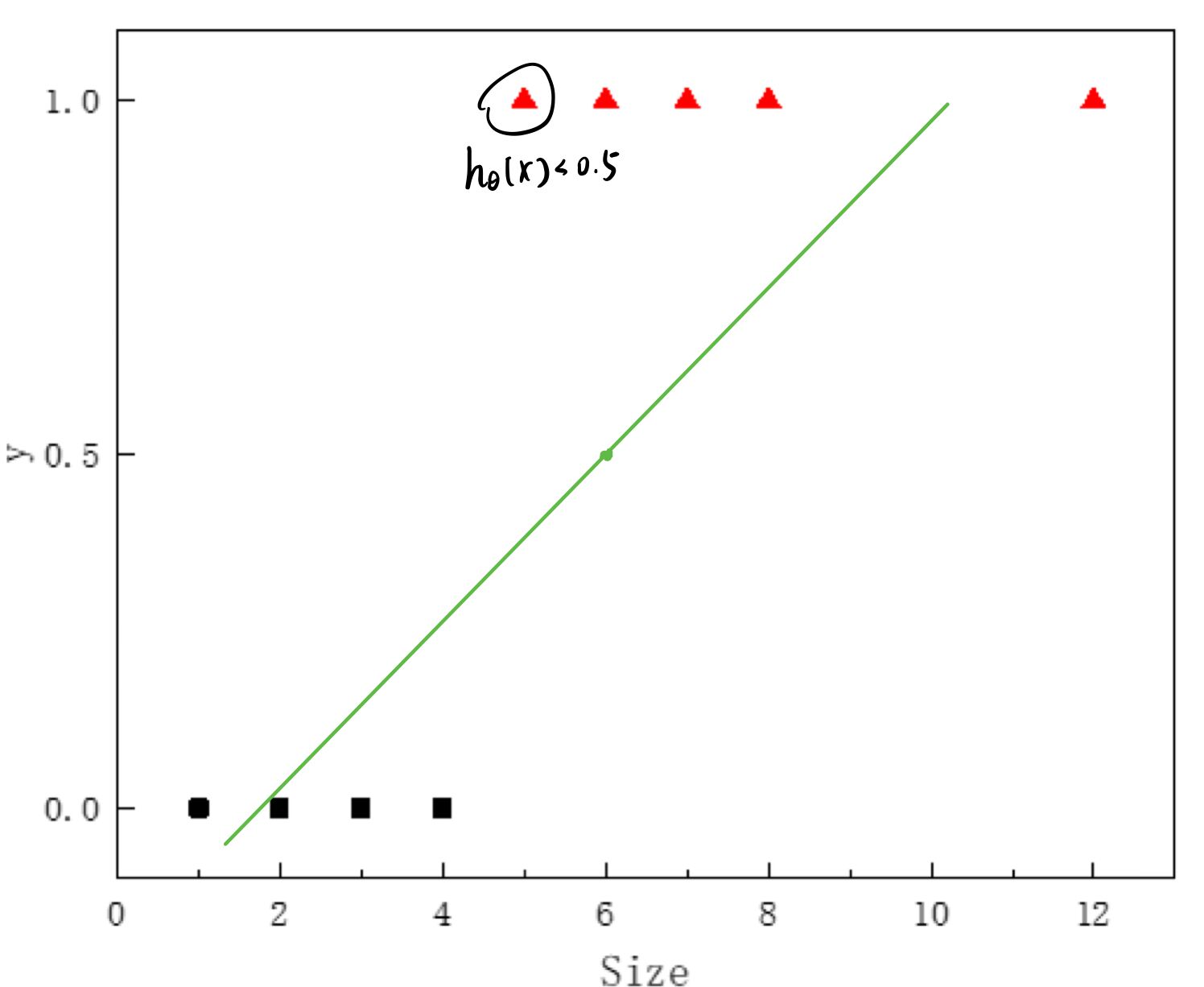
逻辑回归(Logistic Regression)
根据上面的分析可以看出,如果使用线性回归,输出的值是可以小于0或者大于1的。事实上对于一个分类程序来说,输出远小于0和远大于1都是非常奇怪的。逻辑回归的好处之一就是得到的输出是一个0到1的数。即: \[ 0\leq h_{\theta}(x)\leq1 \] 当我们在用线性回归的时候,我们提出的假设是: \[ h_{\theta}(x) = \theta^TX \] 这个式子的意义就是,每一个输入的特征都对结果有一定的贡献,这个贡献的大小就是对应的权重\(\theta_i\)。为了让输出结果为在0到1之间,同时又要体现各个特征的贡献,那么聪明的人们就想到用以下形式来作为输出函数: \[ h_{\theta}(x) = g(\theta^TX)\\ g(z) = \frac{1}{1+e^{-z}} \] 函数\(g(z)\)被称为\(Sigmoid\)函数,图像如下图所示:
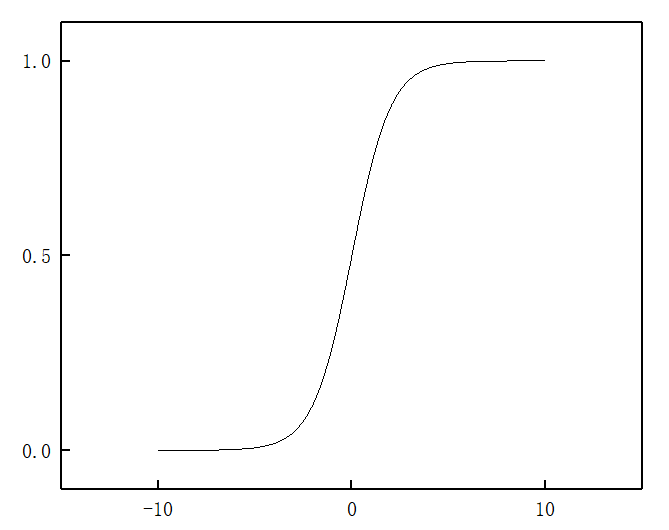
显然,这个函数的值最终都是在区间\((0,1)\)上的。也就是说这个函数实现了所有实数到区间\((0,1)\)上的映射。我们再联想一下,这个一定在区间\((0,1)\)上的输出值,会有什么意义呢?当然可以解释成靠近0或1的程度,而这种程度,很直觉地,非常类似于概率。也就是说,我们得到的\(h_{\theta}(x)\),可以认为是分类结果为1的概率。用数学形式表示如下: \[ h_{\theta}(x) = P\{y=1|x; \theta\} \] 好的,那么我们已经知道了使用的函数的形式及其意义,接下来我们介绍一下决策边界(Decision Boundary)。
决策边界(Decision Boundary)
再把\(Sigmoid\)函数搬出来,仍记得它长成这样:
\[
g(z) = \frac{1}{1+e^{-z}}
\] 
显然,如果我们把\(z = 0\)代入函数式中,得到的函数值为0.5,也就是说
- \(z\geq0:\ g(z)\geq0.5\)
- \(z<0:\ g(z)<0.5\)
显然,要分类0和1,只要将\(g(z)\)的大小与0.5作比较即可,也就是比较\(z\)与0的大小关系。 前面提到,\(z = \theta^TX\),那么整个过程就简化为:
- \(\theta^TX\geq0\): 类别1
- \(\theta^TX<0\): 类别0
有没有联想到什么?或许还不够明显,如果写成如下形式呢? - \(\theta_1x_1 + \theta_2x_2+\dots+\theta_nx_n\geq0\): 类别1 - \(\theta_1x_1 + \theta_2x_2+\dots+\theta_nx_n<0\): 类别0
或许高维还是有些不够直观,降到二维看一看? - \(\theta_1x + \theta_2y\geq0\): 类别1 - \(\theta_1x + \theta_2y<0\): 类别0
这个形式,是不是非常像我们高中学到过的线性规划呢?回想一下线性规划的思路,先令整个表达式等于0,在坐标系中画出一条线,将整个坐标空间划分成两个部分,一部分满足表达式>0,另一部分则满足表达式<0。事实上,这一条线就可以叫做决策边界(Decision Boundary)。拓展至三维还是可以想象的,那时候决策边界就是一个平面,但是当维度拓展至四维时,我们就难以将其具象化了,但是这种思想依旧是正确的。我们把满足\(\theta_1x_1 + \theta_2x_2+\dots+\theta_nx_n=0\)的所有点组成的集合叫作超平面(Hyperplane),它也就是决策边界了。
那么,一切的一切,又落在确定决策边界这个问题上了。
要确定决策边界,也就是要确定最合适的参数\(\theta\)。还是那句话,何为==合适==,使得训练集对应的Loss函数最小,就是合适。
损失函数(Loss Function)
试试线性回归的Loss Function?
学习了线性回归的相关知识,我们很容易想到继续用MSE来表示,即: \[ L(\theta) = \frac{1}{m}\sum_{i=1}^m\frac{1}{2}(h_\theta(x^{(i)})-y)^2 \] (注: 此处的系数\(1/2\),只是为了让求导后的形式更简洁而已,对理解Loss函数没有实质影响) 然而,经过各种学者的探索与验证,我们发现,这种形式的函数是一个非凸函数(non-convex function)。我们把求和号后面的式子视为函数\(Cost(h_\theta(x^{(i)}),y)\),则Loss Function可以精简成如下格式: \[ L(\theta) = \frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y)\\ Cost(h_\theta(x),y)=\frac{1}{2}(h_\theta(x)-y)^2 \]
这里借用一下吴恩达机器学习课程里的图,函数的图像轮廓大概如下:
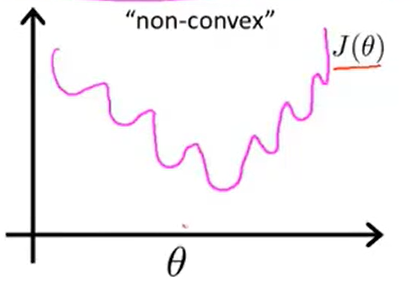
显然,这种函数有非常多的局部最优(Local Minimum),较难收敛到全局最优。那么我们真正用到的Cost函数是: \[ Cost(h_\theta(x),y) = \left\{ \begin{aligned} -log(h_\theta(x))& \ \ \ \ if\ \ y =1 \\ -log(1-h_\theta(x))& \ \ \ \ if\ \ y=0 \end{aligned} \right. \] 历史已经向我们证明了这个Cost函数是可行的。或许很多教程都会直接把这个结果给出来,但是,为什么呢?
Maximum Likelihood
我们已经知道,输出的\(h_\theta(x)\)表示的是输入为\(x\),输出为1的概率。那么,改变\(\theta\)的时候,一个类别为1的样本,预测结果为1的概率越高,则这个训练的模型越准确。那么如果有两个类别为1的样本,则是两个预测结果都为1的概率越高,那么这个训练的模型越准确。以此类推,假设有m个类别为1的样本,全部的预测结果都是1的概率越高,这个训练的模型越准确。对类别为0的样本也是同理。换句话说,所有样本的预测结果都与事实匹配的概率越高,那么模型越准确。 那么我们的目的就是找出合适的参数\(\theta\),使得下式最大: \[ P\{h_\theta(x^{(1)})=y^{(1)}\}\cdot P\{h_\theta(x^{(2)})=y^{(2)}\}\dots P\{h_\theta(x^{(m)})=y^{(m)}\} \] 上式就被称为Likelihood。我们可以把获得的所有训练集数据当作一次试验,\(m\)为一次试验中样本的数量。整个过程也就可以理解成,我们不停地寻找参数\(\theta\),使得在这个条件下,做一次试验能得到和训练集一模一样的数据的概率最大。
我们知道,\(h_\theta(x)\)可以理解为判断\(x\)为类别1时的概率,那么显然地,\(1-h_\theta(x)\)为判断\(x\)为类别0的概率。为了更好地理解,举一个例子吧,假设训练集有四组数据,对应的类别如下表:
| \(x^{(1)}\) | \(x^{(2)}\) | \(x^{(3)}\) | \(x^{(4)}\) |
|---|---|---|---|
| Class 1 | Class 0 | Class 0 | Class 1 |
那么对于这个训练集,Likelihood就可以写成如下形式: \[ h_\theta(x^{(1)})\cdot (1-h_\theta (x^{(2)}))\cdot h_\theta(x^{(3)})\cdot (1-h_\theta (x^{(4)})) \] 那么问题来了,要求极值就肯定涉及求导,这么多函数相乘,要求导实在是太过复杂,那么这里我们就可以运用到高中学过的用对数进行降级运算。上面的思路就转化为要使下式达到最大值: \[ ln(h_\theta(x^{(1)}))+ ln(1-h_\theta (x^{(2)}))+ ln(h_\theta(x^{(3)}))+ ln(1-h_\theta (x^{(4)})) \] OK,那现在求导应该方便一点了。但是还是有点怪怪的,我们已经知道了梯度下降算法,但是那是用来求最小值的,现在我们要求最大值,怎么办呢?每一项加一个负号就可以了。 \[ -log(h_\theta(x^{(1)}))- log(1-h_\theta (x^{(2)}))- log(h_\theta(x^{(3)}))- log(1-h_\theta (x^{(4)})) \] P.S. 笔者百度了一下,发现逻辑回归里确实也有梯度上升法,这里就不详细展开了,读者有兴趣可以了解一下。
好了,那么现在再回到我们的Cost函数,是不是就一目了然了呢。 \[ Cost(h_\theta(x),y) = \left\{ \begin{aligned} -log(h_\theta(x))& \ \ \ \ if\ \ y =1 \\ -log(1-h_\theta(x))& \ \ \ \ if\ \ y=0 \end{aligned} \right. \]
Loss函数的一般形式
注意到,我们的Cost函数是一个分段函数,而分段函数的求导是非常复杂的。再考虑到\(y\)的取值只有0和1,我们可以把Cost函数写成一个比较容易求导的形式: \[ Cost(h_\theta(x),y) = -ylog(h_\theta(x)) -(1-y)log(1-h_\theta(x)) \] 那么Loss函数就是如下形式: \[ L(\theta) = \frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)}) =\frac{1}{m}\sum_{i=1}^m[-y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-h_\theta(x^{(i)}))] \]
总结
具体的计算部分就留到下篇文章再详细阐述吧。也确实还有很多东西没讲,比如多分类问题、以及逻辑回归与线性回归的巧合之类的。这篇文章提到的的很多知识都很有意思,包括决策边界的提出,对数降级运算的思想以及最后Cost函数的一般形式,这不是小聪明,这是大智慧啊!
勘误历史
2021.03.11 感谢用户ah_atishoo对\(Sigmoid\)函数表达式的勘误!