线性回归:机器学习的“Hello, World“
想要解决的问题
假设我们知道若干房子的面积以及对应的房价,那么如果随便告诉我们一套房子的面积,怎么才能知道这套房子最可能买多少钱呢?再假设我们知道了一些零件的使用时间和对应的维修费用,那么如果告诉我们一个零件的使用时间,我们要怎样推测出来对应的维修费用呢?没错,线性回归就是用来解决这些问题的,也就是通过拟合曲线来进行预测。
线性回归(Linear Regression)
线性回归大体分为三个部分,选择合适的模型(model),确定损失函数,梯度下降求解最优参数。
选择模型(Model)
首先我们要知道模型(model)是什么,在这个问题中,我们所说的model是指一个函数族。我们最终想要的结果,就是输入一个\(x\),得到一个十分可信的输出\(\hat{y}\),其实也就是找一个比较好的函数而已。问题是,这种函数可能有非常多,以单变量线性回归为例子,我们可以提出以下函数来进行拟合: \[ \begin{aligned} \hat{y} &= \theta_0 + \theta_1 x \\ \hat{y} &= \theta_0 + \theta_1 x + \theta_2 x^2\\ \hat{y} &= \theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3\\ \vdots \end{aligned} \] 同样地,我们挑一个最简单的,也就是第一个函数。 \[ \hat{y} = \theta_0 + \theta_1 x \]
很显然,我们的最终目标就是找出\(\theta_0\)和\(\theta_1\)使得这个函数足够准确。那么问题又来了,我们要怎么样判断这个函数是否足够准确呢?
损失函数(Loss function)
我们在说准确这个词的时候,实际上是在讨论什么?是误差。足够准确,也就是说误差足够小。损失函数(Loss function)就是用来描述这个误差的。如果要衡量误差,直接用预测值减去实际值就可以得出来了,如下: \[ \delta = \hat{y} - y \] 对于单个数据点我们当然可以这样做,那对于一堆数据点呢?一个很简单的想法就是直接将多个点的误差相加,问题是如果正的误差和负的误差相加起来抵消掉了怎么办。比如我们现在测量一个5cm的木块,第一次测出来是4.9cm,此时的误差就是-0.1cm,第二次测出来是5.1cm,此时的误差就是0.1cm。两次误差加起来就是0了,那岂不是相当于没有误差?那么现在聪明的你应该会想到,可以用绝对值。没错,这确实是一个可以选择的方式,然而,在实际应用中,带有绝对值的变量往往在求导等操作上会有一点麻烦。所以我们选用另一种方法,就是把这个数平方,即: \[ \delta = (\hat{y} - y)^2 \] 同样,上式也是对一个数据点的计算,如果有多个数据点,假如一共有\(m\)个,直接相加的话,得到的就是所有数据点的误差之和了,但是当数据点非常多时,这个数字就变得很大了,为了方便计算,我们在前面再除以一个数据点的数量,也就得到了我们的损失函数(Loss function): \[ L(\theta_0, \theta_1) = \frac{1}{m}\sum_{i=1}^m(\hat{y}^{(i)} - y)^2 \] (\(\hat{y}^{(i)}\)里的上标\((i)\)表示第\(i\)个数据点) 好的,那么现在我们会发现数学符号逐渐多了起来,但是没有关系,我们把整个过程捋一捋。
还记得我们的model吗?就是下面这个: \[ \hat{y} = \theta_0 + \theta_1 x \] 我们的任务是什么,就是找到最合适的\(\theta_0\)和\(\theta_1\),使得上式可以取得较好的预测结果。怎么评估这种合适程度呢,我们将会用Loss函数来描述。不断改变\(\theta_0\)和\(\theta_1\)的值,利用手上已有的数据 \(\{ (x^{(1),} y^{(1)}), (x^{(2),} y^{(2)}), (x^{(3),} y^{(3)}), \dots, (x^{(m),} y^{(m)}) \}\)计算出Loss函数的值即可。那么什么时候才算是找到了最合适的\(\theta_0\)和\(\theta_1\)呢,显然,就是Loss函数最小的时候。误差最小就代表最准确,这是非常明显的。
那么接下来,我们会介绍一种求解\(\theta_0\)和\(\theta_1\)的最常用的方法,梯度下降法(Gradient Descent)。
梯度下降法(Gradient Descent)
经过高中数学的学习,想必大家都知道了导数的几何意义,在某一点的导数就等于过这一点切线的斜率,如下图所示:
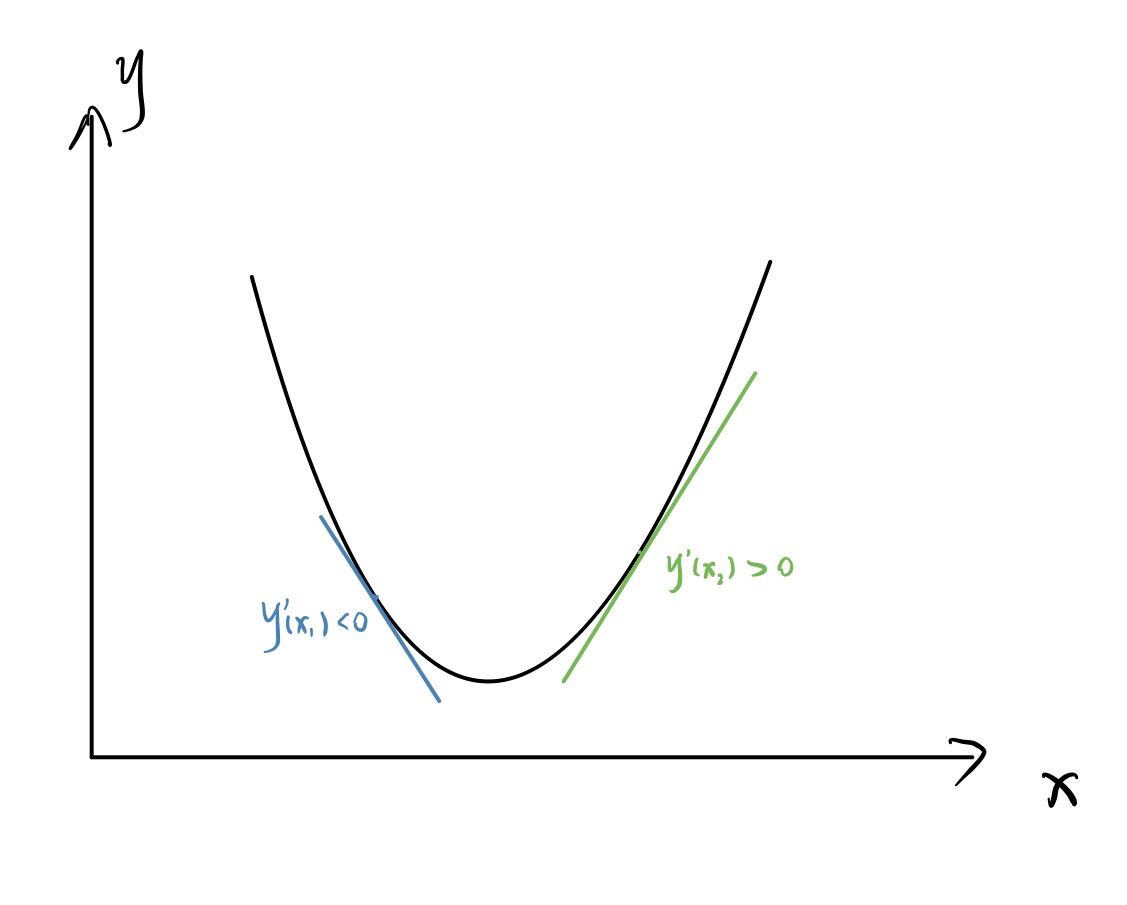
显然,在\(x_1\)处的导数小于0,意味着在这个点的右边还有会使\(y\)更小的\(x\)值,暗示我们向右取值;相反地,在\(x_2\)处的导数大于0,意味着在这个点的左边有能使\(y\)更小的\(x\)值,暗示我们向左取值。所以就有如下的迭代策略: \[ \theta_j := \theta_j - \eta \frac{\partial}{\partial \theta_j}L(\theta_0, \theta_1) \ \ \ \ \ \ \ \ (j = 0, 1) \] 公式逐渐复杂了起来,不过问题不大,我们来分析一下各个参数的意义。
\(\theta_j\):就是代指\(\theta_0\)和\(\theta_1\)
\(:=\)是赋值的意思,让左边的数等于右边的数
\(\eta\):学习率(Learning
Rate),把降低Loss函数的过程比喻成下山,那么学习率\(\eta\)就是下山的步长,步子跨大了容易扯着蛋,步子跨大了就可能一步走到另外一边的上坡路去了,但是步子小了就会走得很慢。
\(\frac{\partial}{\partial \theta_j}L(\theta_0, \theta_1)\):Loss函数对\(\theta_j\)的偏导,可以大概理解为其余变量为常数时,对单变量的导数。
总的来说,整个过程我们就是在变化\(\theta_0, \theta_1\),利用训练集(Training Data)来让我们的“假想函数”与实际的差距越来越小。
求导公式
我们这里把Loss函数的形式写完整: \[ L(\theta_0, \theta_1) = \sum_{i=1}^m(\hat{y}^{(i)} - y)^2 = \sum_{i=1}^m(\theta_0+\theta_1x^{(i)}-y^{(i)})^2 \] 那么两个参数的偏导数就如下所示: \[ \frac{\partial}{\partial \theta_0}L(\theta_0, \theta_1)=\frac{2}{m} \sum_{i=1}^m(\theta_0+\theta_1x^{(i)}-y^{(i)}) \]
\[ \frac{\partial}{\partial \theta_1}L(\theta_0, \theta_1)=\frac{2}{m} \sum_{i=1}^m(\theta_0+\theta_1x^{(i)}-y^{(i)}) \cdot x^{(i)} \]
拓展(幂次)
Loss函数构造的思想依然是一样的,只是我们选取的model发生变化了,当然,也就意味着偏导数的形式也发生变化了。假设我们一开始选取的model如下: \[ \hat{y} = \theta_0 + \theta_1 x + \theta_2 x^2 + \dots + \theta_n x^n \] 那么偏导数的形式变为: \[ \frac{\partial}{\partial \theta_0}L(\theta_0, \theta_1, \dots, \theta_n)=\frac{2}{m} \sum_{i=1}^m(\theta_0+\theta_1x^{(i)}+\dots + \theta_n x^{(i)n}-y^{(i)}) \]
\[ \frac{\partial}{\partial \theta_j}L(\theta_0, \theta_1, \dots, \theta_n)=\frac{2}{m} \sum_{i=1}^m(\theta_0+\theta_1x^{(i)}+\dots + \theta_n x^{(i)n}-y^{(i)})\cdot x^{(i)j} \]
其中\(j\)取\(1, 2, \dots, n\).