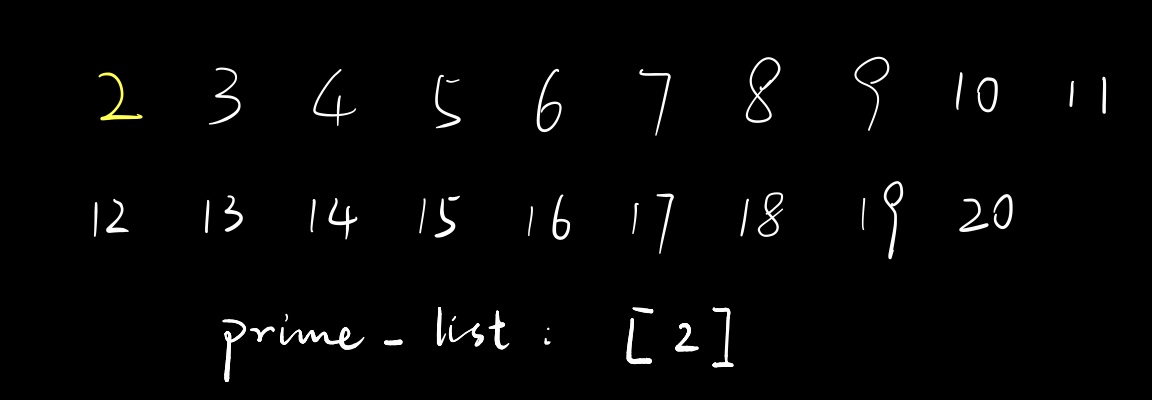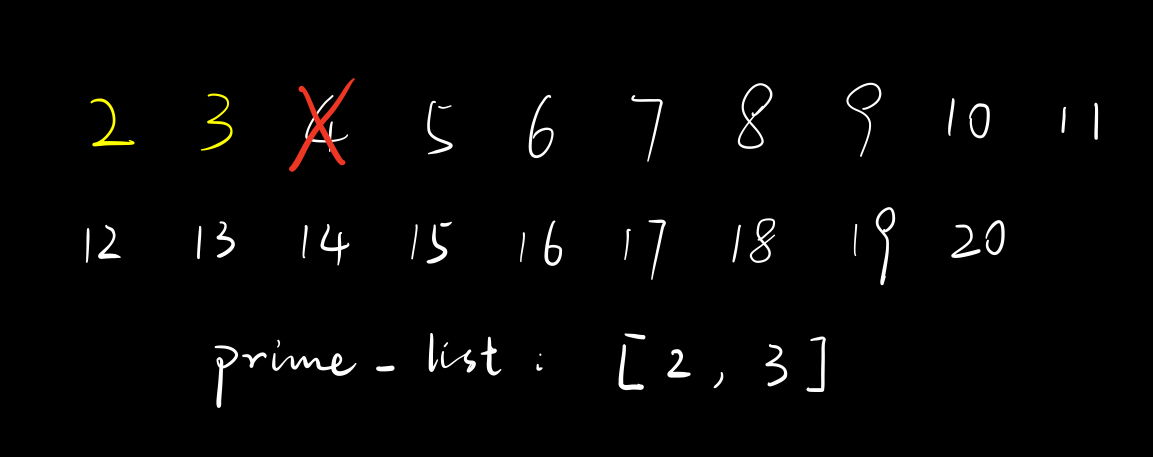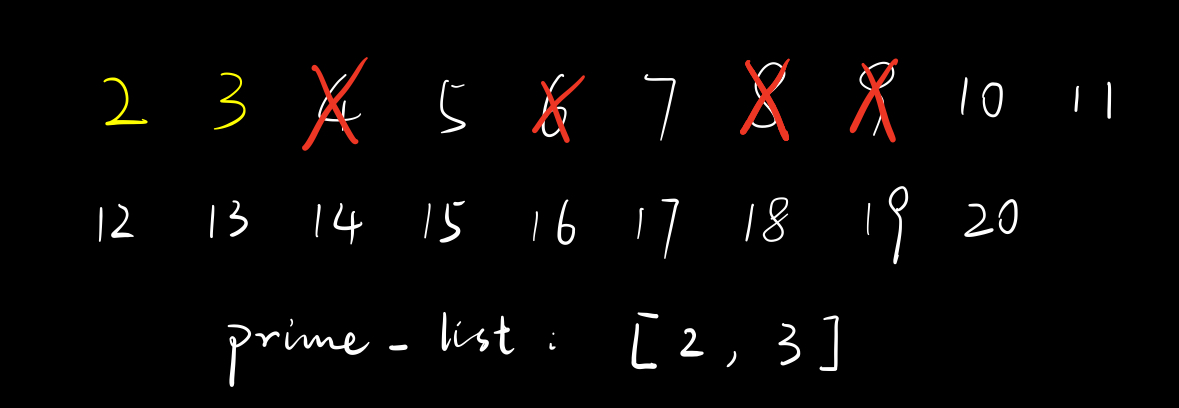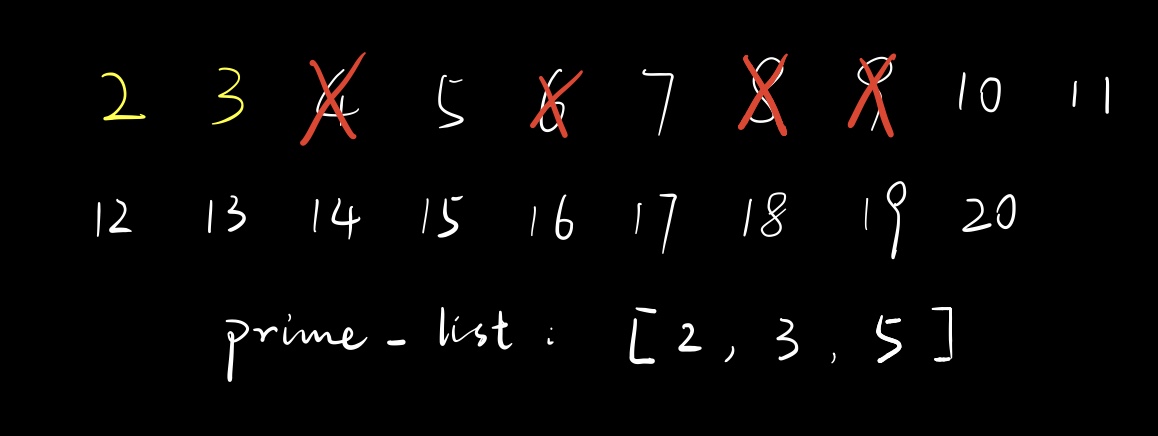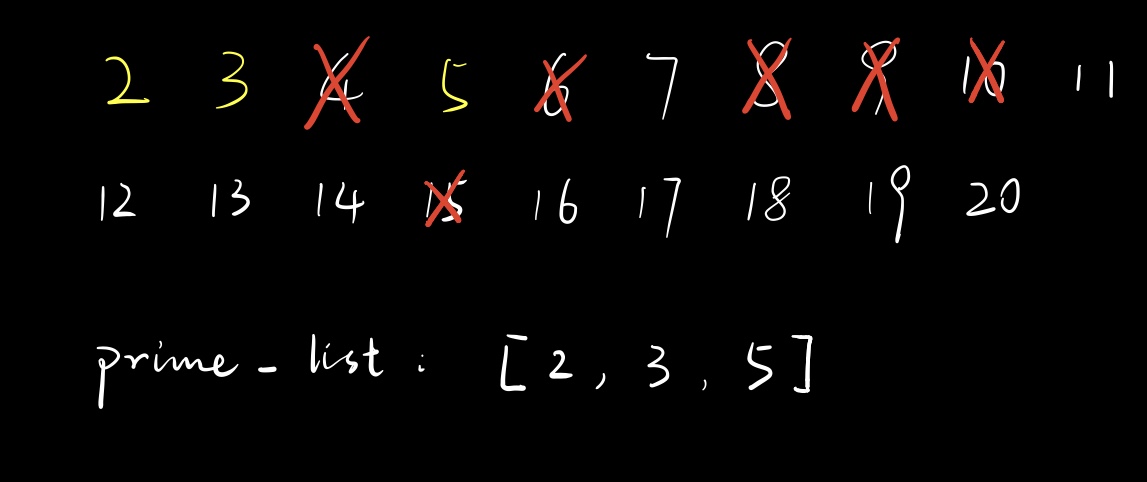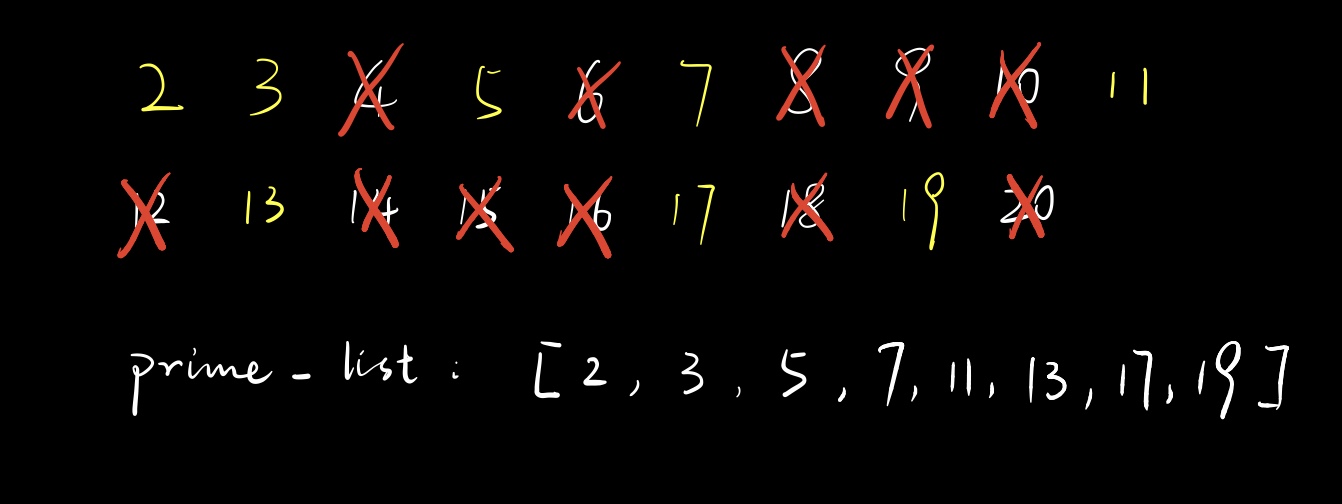之前介绍了Eratosthenes筛法，时间复杂度是$O(nloglogn)$。比起最朴素的遍历法，这个时间复杂度已经不错了。然而，在建立质数表的时候，仍然会有重复计算。比如，我们遍历到$2$的时候，会筛掉指定范围中$2$的所有倍数，当然也就会筛掉$12$这个数，然后遍历到$3$，同样也会筛掉$12$这个数，类似这种的重复计算还是挺多的。那么要怎样才能避免掉这些重复计算，优化时间复杂度呢？

欧拉筛法

欧拉筛法，又称为线性筛，从这个名字就可以知道这个方法的时间复杂度是$O(n)$。欧拉筛法的思想就是，让每个合数只被它的最小质因数筛去。这样讲多少有点抽象了，我们接下来介绍一下整个欧拉筛法的流程。

首先明确一下目标，我们要得到$2\sim n$之中的所有素数。筛法的思想仍然是筛掉素数的倍数，不过这次，我们并不会像埃氏筛法那样，把前方的合数赶尽杀绝。欧拉筛法最妙的地方，就是及时收刀。如果我预测到你未来会挂掉，那何必脏了自己的剑呢。

篇幅所限，我们先以$2\sim 20$这个范围为例。

在开始遍历之前，我们需要准备好两个数组。$is_prime$用来标记对应下标是否为素数，$prime_list$用来存放这个范围里所有的素数。

与埃氏筛法相同，我们要先假设这个范围内所有的数都是素数，就是将$is_prime$全部置为$true$。然后开始遍历。

对于$2$，根据查询$is_prime$，我们知道它是素数，把它放进$prime_list$里。

此时遍历$prime_list$，只有一个$2$，于是我们筛掉$2\times 2$，即$4$，把$is_prime[4]$设为$false$。然后我们就开始遍历下一个数了。可能有人会好奇，那后面的$6$和$8$之类的这些数，不都是$2$的倍数吗，为什么不筛掉？这就是我前面提到的妙处了——我们知道这些数在未来会被筛掉。别着急，先往下看。

对于$3$，根据查询$is_prime$，我们知道它是素数，把它放进$prime_list$里。

此时遍历$prime_list$，有$2$，于是筛掉$3\times 2$；有$3$，于是筛掉$3\times 3$。把$is_prime[6]$和$is_prime[9]$设为$false$。

接着遍历到$4$，查询$is_prime$，我们知道它不是素数，所以不会放进$prime_list$中。

此时遍历$prime_list$，先是$2$，于是筛掉$4\times 2$，将$is_prime[8]$设为$false$。然而，由于$4$是$2$的倍数，所以我们在此停止$prime_list$的遍历。

这个停下来的过程，就是我前面提到的“收刀”。我们假设没有停下来，那我们在这里就会筛掉$4\times 3 = 12$。然而，当我们在外面的大循环里遍历到$6$时，我们也会筛掉$6\times 2=12$。嗯…这就与我们“避免重复计算”的想法相悖了。思考一下，根据质因数分解，我们知道，每个合数$m$是可以写成若干个质数的乘积的，这些质因数里面，肯定会存在一个最小的$p_{min}$，使得$m = p_{min}\cdot r$，其中$r$为余下质因数的乘积。这种分解方式是唯一的，我们的指导原则就是只根据这种分解方式来筛掉合数。以下是几个具体的例子：

\[\begin{align*} 12 &= 2\times 2 \times 3 = 2\times 6\\ 18 &= 2\times 3 \times 3=2 \times 9 \\ 20 &= 2\times 2 \times 5 = 2\times 10\\ 45 &= 3\times 3 \times 5 = 3\times 15 \end{align*}\]

比如，$4$是$2$的倍数，也就意味着，$4$乘以某个质数$p$，总能分解为$2\times 2p$，那么我们自然可以等遍历到$2p$的时候，再筛掉这个数。

OK，回到我们例题的解答过程，现在我们筛掉了$8$。外层循环遍历到$5$，根据查询$is_prime$，我们知道它是素数，把它放进$prime_list$里。

此时遍历$prime_list$，先是$2$，于是筛掉$5\times 2$，将$is_prime[10]$设为$false$；然后是$3$，筛掉$5\times 3$，将$is_prime[15]$设为$false$；还有个$5$，但是$5\times 5$超出我们要讨论的范围了，所以不用处理。

随后遍历到6，它不是素数，我们筛掉$2\times 6=12$，$6$是$2$的倍数，在此“收刀”，进入下一个数的遍历。

$7$是素数，筛掉$2\times 7=14$，随后的素数与$7$相乘都超出讨论范围，忽略掉。

$8$不是素数，筛掉$2\times 8=16$，随后的素数与$7$相乘都超出讨论范围，忽略掉。

$9$不是素数，筛掉$2\times 9=18$。

$10$不是素数，筛掉$2\times 10 = 20$。

随后的数一旦乘$2$，都超出范围，所以也无法实现“筛”的作用了，于是我们的素数表已建立完毕。

代码实现 (C++ & Python)

C++:

#include<iostream>
#include<vector>
using namespace std;
int main()
{
    int n = 100;
    vector<int> prime_list;
    vector<bool> prime_hash(n+1);
    fill(prime_hash.begin()+2, prime_hash.end(), true);   //要首先假设所有数都是质数，需要事先确定0、1不是质数
    for(int i=2; i<n+1; i++)
    {
        if(prime_hash[i])
            prime_list.push_back(i);
        for(int j=0; j<prime_list.size(); j++)
        {
            if(prime_list[j]*i > n+1) break;
            prime_hash[prime_list[j]*i] = false;
            if(prime_list[j] % i == 0) break;   // 预料到以后定会有人来取后面合数的人头
        }

    }
    for(int i=0; i<prime_list.size(); i++)
    {
        cout << prime_list[i] << endl;
    }
    return 0;
}

Python:

prime_hash = [True for i in range(0, 101)]
prime_hash[0] = prime_hash[1] = False
prime_list = []
for i in range(0, 101):
    if prime_hash[i]:
        prime_list.append(i)
    for p in prime_list:
        if p*i >= 101:
            break
        prime_hash[p*i] = False
        if i%p == 0:
            break
print(prime_list)

复杂度讨论

外层循环肯定要把$2\sim n$遍历一遍，时间复杂度为$O(n)$。现在问题就是我们里层循环到底多做了多少次运算。因为我们整个过程都遵从“所有合数只被筛一次的”原则，那么我们多做的运算其实就是$2\sim n$中合数的个数。整个遍历次数一定小于$2n$，所以时间复杂度可以表示为$O(n)$。